偶遇题目,拼尽全力无法战胜,故来学习
wiki 伪随机数
随机性、熵与随机数生成器:解析伪随机数生成器(PRNG)和真随机数生成器(TRNG)-CSDN博客
【密码学】流密码的基本概念-CSDN博客
MT19937_mt19937predictor-CSDN博客
浅析MT19937伪随机数生成算法-安全KER - 安全资讯平台
你没听过的梅森旋转算法 - CHNmuxii - 博客园
Mersenne Twister 梅森旋转算法笔记 这一篇很详细
相关知识 既然聊到随机数生成了,就会想到PRNG嘛,所以我觉得顺带联系一下流密码会更透彻一点,下面是一些联系知识点,可跳过直接看梅森旋转算法介绍。
流密码 流密码是一种对称密码,一般逐字节或逐比特处理信息(比如说采用异或加密)。现有的流密码是在一次一密 的思想基础上发展来的。
一次一密(One-Time Pad,简称OTP)也是一种流密码算法,它被认为是理论上最安全的加密算法之一,它必须遵循以下原则:
密钥必须和明文一样长
密钥必须是真正随机 的(我们可以采用真随机数发生器TRNG 来生成)
密钥必须只使用一次
密钥必须保密 (感觉有点废话)
看上面这几条原则,很容易就可以想到密钥的管理是困难的。密钥和明文一样长,且每个都只使用一次,密钥的存储和共享十分困难,这在实际运用上是不现实的
于是人们在试图解决一次一密密钥管理和长度的问题时,想到了能不能有一种方法,只需要提供一小段密钥,就可以生成加密明文所需要的所有密钥。流密码就在此思想上发展。
在流密码中,一个小的密钥(通常称为种子 或初始向量)被用来通过一个伪随机数生成器(PRNG) 产生一个与明文等长的伪随机密钥流 。这个密钥流然后与明文进行异或 操作,生成密文。同样,解密过程就是用相同的密钥流对密文进行异或,恢复出明文。
像我们学过的比较简单的流密码RC4、LCG(也都是PRNG生成算法)都是采用这种思想。(我的理解是,一种流密码,其实就是一种PRNG生成算法,毕竟加密一般就是异或嘛,所以还是要看伪随机数的生成)
PRNG 我们将要了解的这个算法,其实就是一种用于生成PRNG(即伪随机数生成器 pseudo random number generator)的一种算法。与PRNG相对的就是TRNG(真随机数生成器),这里不做过多介绍。
PRNG可以使用 随机种子 序列 。PRNG的周期定义为:序列的无重复前缀长度在所有起始状态中的最大值。周期受状态数的限制,通常用比特位数表示。然而,每增加一个比特位,周期长度就可能增加一倍,所以构建周期足够长的PRNG对于许多实际应用程序来说是很容易的。(感觉有点绕,但是目前只要知道,用相同的seed,会生成相同的序列就行了)
PRNG所生成的序列,其特性近似于随机数序列。具有以下特点:
确定性,相同的种子值会生成相同的序列
高效性,PRNG能快速产生大量随机数
周期性,PRNG会在一定周期后重复,但是现代PRNG算法这个周期是很长的
分类 目前通用的伪随机数生成器主要有
线性同余生成器,LCG
线性回归发生器
Mersenne Twister (梅森旋转算法)
xorshift generators
WELL family of generators
Linear feedback shift register,LFSR,线性反馈移位寄存器
后面翻资料的时候发现还有一种密码学PRNG(CSPRNG) :密码学伪随机数生成器(Cryptographically Secure Pseudo-Random Number Generator, CSPRNG),只能后面再去了解了。LFSR之前做题也有遇到,只能又鸽了
知道这样一个框架后,就可以进入重头戏,PRNG的一种算法——梅森旋转算法
介绍 梅森旋转算法,是由松本真和西村拓士在1997年开发的一种能快速产生优质随机数的算法。
它之所以叫做是梅森旋转算法是因为它的循环节是 $ 2^{19937}-1 $,这个叫做梅森素数。这个循环节(就是循环周期,理解为经过多少次后会回到第一次的随机数)是很长的,这也是为什么这个算法可以产生优质的随机数。
常见的两种形式为基于32位的MT19937-32和基于64位的MT19937-64(其实是状态向量里整数的位数的区别),而python中的random库主要用的还是MT19937-32,所以我们主要理解一下这个
代码实现 MT19937 算法可分为三个部分
初始化 旋转状态 提取伪随机数
其中 32 位的 MT19937 Python 代码实现为:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 def _int32(x): return int(0xFFFFFFFF & x) class MT19937: # 初始化 def __init__(self, seed): self.mt = [0] * 624 self.mt[0] = seed self.mti = 0 for i in range(1, 624): self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i) # 提取伪随机数 def extract_number(self): if self.mti == 0: self.twist() y = self.mt[self.mti] y = y ^ y >> 11 y = y ^ y << 7 & 2636928640 y = y ^ y << 15 & 4022730752 y = y ^ y >> 18 self.mti = (self.mti + 1) % 624 return _int32(y) # 旋转状态 def twist(self): for i in range(0, 624): y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff)) self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624] if y % 2 != 0: self.mt[i] = self.mt[i] ^ 0x9908b0df
其实如果简单过一遍的话,还是好理解的,就是根据一个seed进行初始化624的状态向量,然后旋转(怎么旋转的有点扣不懂了,浅放一下),提取,每624次提取后再旋转
Randon库 了解了基本的原理后,我们来看看Python中random库的诸如getrandbits这些函数的具体用法和小特性
python中内置的Random类就是采用了MT19937算法,每次生成的随机数都是32位的。getrandbits(32)方法可以获得一个32位随机数
1 2 3 4 5 import randomprint (random.getrandbits(32 ))
random.seed(a):设置初始化随机种子,可输出相同随机数序列;a取整数或浮点数,不设置时默认以系统时间为种子
1 2 3 4 5 6 7 8 9 10 11 12 13 14 import randomprint (random.getrandbits(32 ))random.seed(32 ) print (random.getrandbits(32 ))random.seed(32 ) print (random.getrandbits(32 ))
getrandbits(8)获得的是32位随机数的前8位,而在这之后再次使用getrandbits(8)获取的是下一个32位随机数的前8位
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 import randomrandom.seed(32 ) print (hex (random.getrandbits(32 ))[2 :])print (hex (random.getrandbits(32 ))[2 :])random.seed(32 ) print (hex (random.getrandbits(8 ))[2 :])print (hex (random.getrandbits(8 ))[2 :])
getrandbits(64)则是两个32位随机数的拼接,倒序拼接
1 2 3 4 5 6 7 8 9 10 11 12 import randomrandom.seed(32 ) print (hex (random.getrandbits(32 ))[2 :])print (hex (random.getrandbits(32 ))[2 :])random.seed(32 ) print (hex (random.getrandbits(64 ))[2 :])
还需要注意,向高位生长时其实跟小于32位一样是从高位开始取。
1 2 3 4 5 6 7 8 9 10 11 12 13 import randomrandom.seed(32 ) print (hex (random.getrandbits(32 ))[2 :])print (hex (random.getrandbits(32 ))[2 :])random.seed(32 ) print (hex (random.getrandbits(40 ))[2 :])
getstate()的用法(相对应的是setstate())
1 2 3 4 5 6 7 import randomrng = random.Random() rng.seed(32 ) print (rng.getstate())
考点 既然说了是伪随机数,那就说明是有一定规律的,所以我们期望可以通过一些手段来预测随机数
大概理解了一下就是将extract_number过程逆向,看了一遍后是理解了,但是让我复述一遍有点难,但是试着来吧
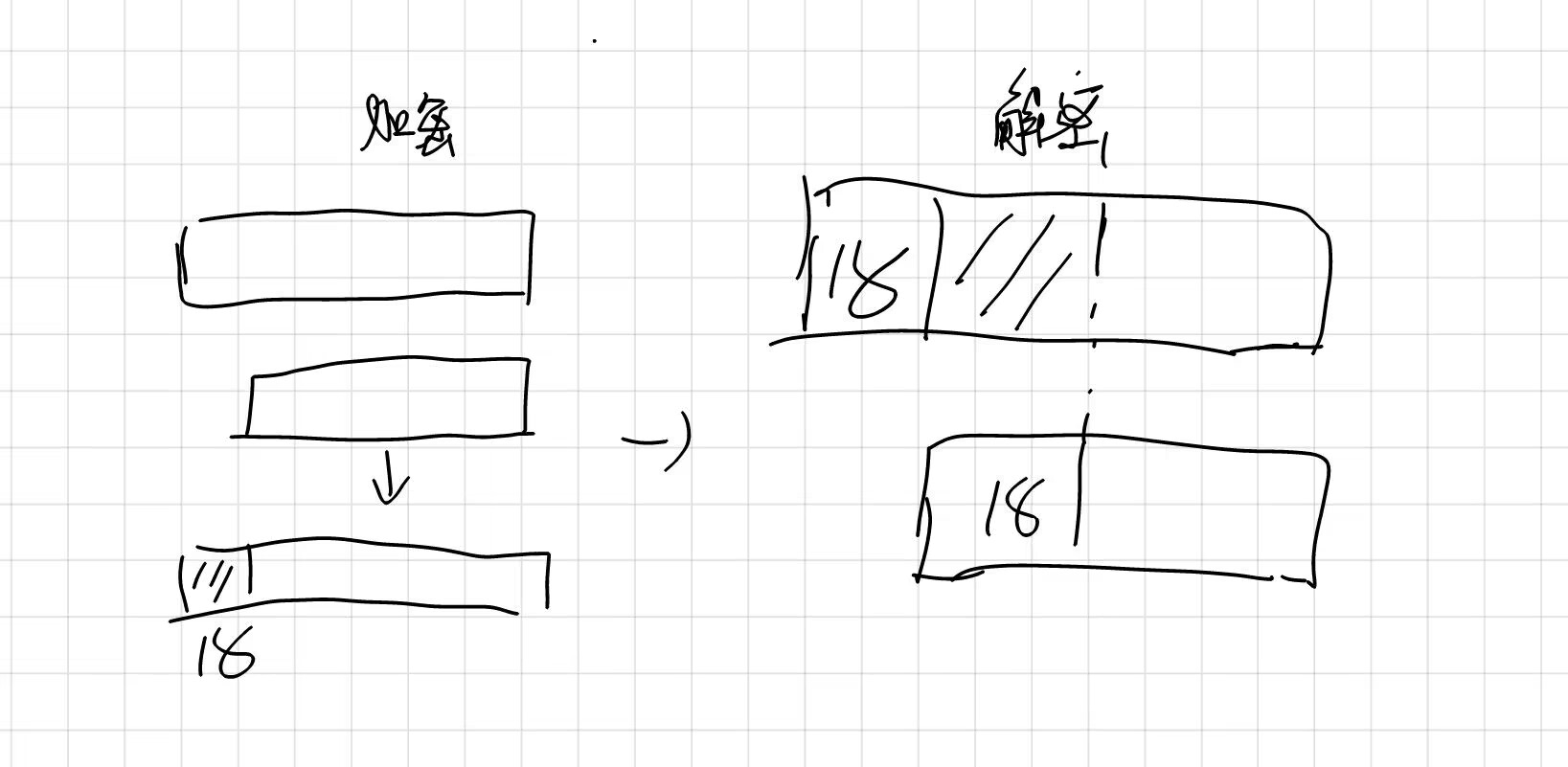
首先 y = y ^ y >> 18这一块,很明显是y和y右移18位后的结果异或,那么高位的18位就是没有变化的,所以我们可以把y_result右移18位后再和自己异或,就又复原了18位,依此类推就可以回退回去,大概是下图这样(图画的有点丑)
代码如下
1 2 3 4 5 6 7 8 9 10 o = 2080737669 print (o.bit_length())y = o^o>>18 for i in range (31 //18 ): y = y^(y>>18 ) print (y==o)
接着我们看y = y ^ y << 15 & 4022730752这个过程,y和 y左移15位与上4022730752 的结果进行异或,相当于y_result的低位15位是原y与y左移15位(其实低位15位都是0)与上4022730752 的结果(图我画不出来,但是就是循环这个过程,低位15知道后再左移15位与上4022730752 ,就又可以知道15位,重复下去)
代码如下
1 2 3 4 5 6 7 8 o = 2080737669 y = o ^ o << 15 & 4022730752 tmp = y for i in range (32 // 15 ): y = tmp ^ y << 15 & 4022730752 print (y==o)
extract_number剩下的两个过程就是一样的分析过程了,这样extract_number就逆向完了
其他几个逆向过程实在扣不动了,放个总代码吧(放过自己)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 class MT19937Recover : def unshiftRight (self, x, shift ): res = x for i in range (32 ): res = x ^ res >> shift return res def unshiftLeft (self, x, shift, mask ): res = x for i in range (32 ): res = x ^ (res << shift & mask) return res def untemper (self, v ): v = self .unshiftRight(v, 18 ) v = self .unshiftLeft(v, 15 , 0xefc60000 ) v = self .unshiftLeft(v, 7 , 0x9d2c5680 ) v = self .unshiftRight(v, 11 ) return v def go (self, outputs, forward=True ): result_state = None assert len (outputs) >= 624 ivals = [] for i in range (624 ): ivals.append(self .untemper(outputs[i])) if len (outputs) >= 625 : challenge = outputs[624 ] for i in range (1 , 626 ): state = (3 , tuple (ivals+[i]), None ) r = random.Random() r.setstate(state) if challenge == r.getrandbits(32 ): result_state = state break else : result_state = (3 , tuple (ivals+[624 ]), None ) rand = random.Random() rand.setstate(result_state) if forward: for i in range (624 , len (outputs)): assert rand.getrandbits(32 ) == outputs[i] return rand mtc = MT19937Recover()
randcrack库进行预测 python中的randcrack库为我们提供了预测的函数,只要我们输入624个32位的数,就可以进行预测
1 2 3 4 5 6 7 8 import random from randcrack import RandCrackrc = RandCrack() for i in range (624 ): rc.submit(random.getrandbits(32 )) print (random.getrandbits(64 ))print (rc.predict_getrandbits(64 ))
但是这个库有个缺点就是必须提交624次,少一次都不行,而且必须是32位的,多一位都不行,具体可以看看下面这篇博客,进行了测试
https://blog.51cto.com/u_16099213/6895353
矩阵状态破解 这个感觉特别巧妙,就是发现了最后的输出和初始状态之间的一个线性关系,然后通过矩阵求解
我们把初始状态state[i]表示为二进制
$ x_0x_1···x_{30}x_{31} $
然后我们把输出的随机数也用二进制表示
$ z_0z_1···z_{30}z_{31} $
二者之间存在以下关系
真不知道这是怎么发现的,只能说太厉害了
那么在GF(2)域上存在一个矩阵使得x变为z
即$ XT=Z $
下面是代码
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 def extract_number (x ): x ^^= x >> 11 x ^^= (x << 7 ) & 2636928640 x ^^= (x << 15 ) & 4022730752 x ^^= x >> 18 return x & 0xffffffff T = [] for i in range (32 ): x = 1 << (31 - i) x = extract_number(x) T.append(x.digits(2 , padto=32 )[::-1 ]) T = matrix(GF(2 ), T) def untemper (leak ): Z = matrix(GF(2 ), ZZ(leak).digits(2 , padto=32 )[::-1 ]) X = T.solve_left(Z) return reduce(lambda x, y: (ZZ(x) << 1 ) + ZZ(y), list (X[0 ]))
如果我们能拿到连续的 624 个输出(比如用 random.getrandbits(32) 连续取 624 次),就能:
1 2 3 4 5 state = [] for _ in range (624 ): output = random.getrandbits(32 ) state.append(untemper(output))
从而恢复初始状态,然后进行预测
然后在m1n9师傅博客上看到另一种脚本写法,思路应该是一样的,这里就直接搬过来喽
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 def construct_a_row (RNG ): row = [] for _ in range (19968 //32 ): tmp = RNG.getrandbits(32 ) row += list (map (int , bin (tmp)[2 :].zfill(32 ))) return row L = [] for i in trange(19968 ): state = [0 ]*624 temp = "0" *i + "1" *1 + "0" *(19968 -1 -i) for j in range (624 ): state[j] = int (temp[32 *j:32 *j+32 ], 2 ) RNG = Random() RNG.setstate((3 ,tuple (state+[624 ]),None )) L.append(construct_a_row(RNG)) L = Matrix(GF(2 ),L) print (L.nrows(), L.ncols()) def MT19937_re (state ): try : R = [] for i in state: R += list (map (int , bin (i)[2 :].zfill(32 ))) R = vector(GF(2 ), R) s = L.solve_left(R) init = "" .join(list (map (str ,s))) state = [] for i in range (624 ): state.append(int (init[32 *i:32 *i+32 ],2 )) RNG1 = Random() RNG1.setstate((3 ,tuple (state+[624 ]),None )) return RNG1 except Exception as e: print (f"[-]{e} " ) pass RNG = MT19937_re()
详细可以上m1n9师傅博客查看
MT19937
暂时看到的就这么多了,其他的等之后补充了
题目 Division(xyctf 2025) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 ''' @File : server.py @Time : 2025/03/20 12:25:03 @Author : LamentXU ''' import random print ('----Welcome to my division calc----' )print (''' menu: [1] Division calc [2] Get flag ''' )while True : choose = input (': >>> ' ) if choose == '1' : try : denominator = int (input ('input the denominator: >>> ' )) except : print ('INPUT NUMBERS' ) continue nominator = random.getrandbits(32 ) if denominator == '0' : print ('NO YOU DONT' ) continue else : print (f'{nominator} //{denominator} = {nominator//denominator} ' ) elif choose == '2' : try : ans = input ('input the answer: >>> ' ) rand1 = random.getrandbits(11000 ) rand2 = random.getrandbits(10000 ) correct_ans = rand1 // rand2 if correct_ans == int (ans): print ('WOW' ) with open ('flag' , 'r' ) as f: print (f'Here is your flag: {f.read()} ' ) else : print (f'NOPE, the correct answer is {correct_ans} ' ) except : print ('INPUT NUMBERS' ) else : print ('Invalid choice' )
一道靶机题,correct_ans = rand1 // rand2这里告诉我们,要想得到flag,我们必须预测出11000位的数整除10000位数的结果,我们回头看random.getrandbits(32)就可以知道,我们有办法搞到624个32位结果,那么运用randcrack库很容易就可以进行预测,交互代码甚至是ai给我写的,解题代码如下
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 from pwn import *from randcrack import RandCrackproc = remote('host' , port) rc = RandCrack() for _ in range (624 ): proc.sendlineafter(b': >>> ' , b'1' ) proc.sendlineafter(b'input the denominator: >>> ' , b'1' ) line = proc.recvline().decode().strip() numerator = int (line.split('//' )[0 ]) rc.submit(numerator) rand1 = rc.predict_getrandbits(11000 ) rand2 = rc.predict_getrandbits(10000 ) correct_ans = rand1 // rand2 proc.sendlineafter(b': >>> ' , b'2' ) proc.sendlineafter(b'input the answer: >>> ' , str (correct_ans).encode()) proc.interactive() ''' WOW Here is your flag: XYCTF{3bb2de1f-5bb3-486a-8da4-d1df6629067b} '''
总结 写了两三天总算写完,但是应该还是不全,之后看有空再修修补补吧,不过总算了解了这么一个东西吧,道阻且长捏