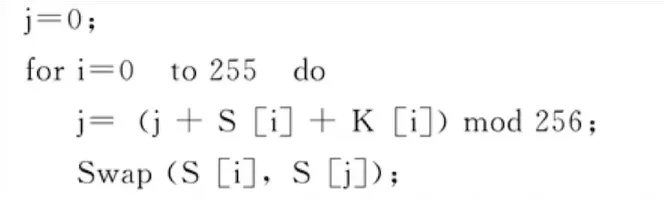对称密码—流密码

RC4

加密流程

初始化算法(KSA)

Step1：先生成一个key，自定义。

Step2：生成一个S盒，S盒有256个元素，分别是0，1，2，······，255。

Step3：生成一个K盒，同样是256个元素，这个K盒用key来填充，如果key是345，那么就3，4，5，3，4，5，3，4，5······这样一直重复填充下去。

Step4：利用K盒来打乱我们刚刚生成的S盒，这个是通过一个规定的转换式子，每做一次，就交换S盒里的两个值。

eg：按上面我们那个K表打乱后的S表如下，大家可以自己试一下（循环了七次）

伪随机子密码生成算法（PRGA)

这一步是为了生成一个新盒，这个新盒里是一些伪随机的子密码，用来加密我们的明文，这个生成过程也有规定的式子，如下

上图是用我们之前的K盒直接存储新生成的伪随机子密码，这无可厚非，只要S盒初始化过后（打乱后）K盒就没什么用了。

之后就是加密过程，就是用我们最后得到的那个子密码来和明文做异或，得到密文。

例题

notRC4

题目

from hashlib import md5
from secret import flag

class Oo0:
    def __init__(self):
        self.O0 = [0] * 256
        self.Ooo = 0
        self.Ooo0 = [0] * 256
        for i in range(256):
            self.O0[i] = i
        self.oO0 = 0

    def OO0(self, oO0):
        l = len(oO0)
        for i in range(256):
            self.Ooo0[i] = oO0[i % l]
        for i in range(256):
            self.oO0 = (self.oO0 + self.O0[i] + self.Ooo0[i]) % 256
            self.O0[i], self.O0[self.oO0] = self.O0[self.oO0], self.O0[i]
        self.Ooo = self.oO0 = 0

    def OO0o(self, length):
        O = []
        for _ in range(length):
            self.Ooo = (self.Ooo + 1) % 256
            self.oO0 = (self.oO0 + self.O0[self.Ooo]) % 256
            self.O0[self.Ooo], self.O0[self.oO0] = self.O0[self.oO0], self.O0[self.Ooo]
            t = (self.O0[self.Ooo] + self.O0[self.oO0]) % 256
            O.append(self.O0[t])
        print(self.O0)
        return O


def xor(s1, s2):
    return bytes(map((lambda x: x[0] ^ x[1]), zip(s1, s2)))


def enc(msg):
    Oo0oO = Oo0()
    Oo0oO.OO0(md5(msg).digest()[:8])
    O0O = Oo0oO.OO0o(len(msg))
    return xor(msg, O0O)


print(enc(flag))
'''
s = [166, 163, 208, 147, 181, 152, 69, 90, 253, 114, 150, 255, 218, 220, 34, 74, 63, 201, 70, 115, 233, 96, 43, 169, 103, 191, 14, 149, 143, 25, 105, 93, 199, 246, 51, 75, 20, 5, 107, 3, 52, 135, 111, 139, 113, 47, 184, 76, 161, 174, 23, 30, 173, 72, 198, 56, 85, 55, 106, 126, 244, 223, 104, 29, 112, 148, 219, 118, 165, 59, 98, 175, 125, 100, 17, 16, 108, 6, 214, 140, 130, 206, 89, 62, 4, 236, 251, 91, 28, 45, 18, 53, 1, 144, 193, 133, 73, 44, 57, 88, 250, 204, 177, 67, 120, 21, 79, 71, 2, 185, 211, 200, 65, 234, 117, 9, 226, 142, 230, 209, 132, 248, 242, 196, 101, 81, 238, 247, 119, 179, 131, 229, 94, 50, 22, 183, 24, 158, 190, 222, 155, 172, 19, 12, 225, 10, 189, 232, 146, 227, 212, 210, 31, 164, 138, 78, 122, 176, 121, 0, 194, 186, 162, 160, 188, 168, 216, 153, 37, 252, 127, 145, 33, 82, 58, 170, 61, 254, 136, 207, 8, 237, 159, 36, 239, 95, 178, 167, 182, 102, 27, 123, 60, 129, 42, 26, 99, 39, 97, 40, 235, 205, 7, 49, 202, 197, 109, 195, 245, 171, 180, 15, 46, 83, 48, 156, 92, 249, 38, 32, 203, 41, 124, 54, 217, 134, 154, 35, 157, 128, 137, 221, 84, 86, 215, 213, 80, 11, 116, 141, 241, 64, 224, 87, 77, 187, 68, 192, 151, 240, 13, 228, 231, 66, 110, 243]
enc = b"]7\xab\xc9\xd8\x90\x1f\xd2OP\xad\x87'0\xe1\xff=~"
'''

考点：rc4，异或

https://cn-sec.com/archives/3093479.html 可以参考这篇博客理解

https://www.bilibili.com/video/BV1G64y1Y7p4/?spm_id_from=333.337.search-card.all.click&vd_source=a01a62f772bf2e577e11004dfef0bde1 这个视频也很棒

虽然题目是notRC4，但流程上就是RC4，所以先了解一下RC4的过程。

首先是初始化算法(KSA)

首先生成一个S盒，S盒有256个元素，分别是0，1，2，······，255，对应题目以下代码（代码只截取重要部分，建议定位到题目中分析）

self.O0 = [0] * 256
for i in range(256):
            self.O0[i] = i

再生成一个K盒，同样是256个元素，这个K盒用key来填充，如果key是123，那么就1，2，3，1，2，3，1，2，3······这样一直重复填充下去，直到填充完毕，对应下面代码

self.Ooo0 = [0] * 256
def OO0(self, oO0):
    for i in range(256):
        self.Ooo0[i] = oO0[i % l]

接着我们要利用K盒来打乱我们刚刚生成的S盒，这个是通过一个规定的转换式子，每做一次，就交换S盒里的两个值，如下

因为S[i]是固定的，所以打乱完全取决于K盒，打乱后的S盒我们称为初始化后的S盒，对应以下代码

for i in range(256):
           self.oO0 = (self.oO0 + self.O0[i] + self.Ooo0[i]) % 256
           self.O0[i], self.O0[self.oO0] = self.O0[self.oO0], self.O0[i]
       self.Ooo = self.oO0 = 0		# 这里是为了后面的使用，所以再次赋0，主要是上面部分

接着是伪随机子密码生成算法（PRGA)、加密阶段

这一步是为了生成一个新盒，这个新盒里是一些伪随机的子密码，用来加密我们的明文，这个生成过程也有规定的式子，如下

上图是用我们之前的K盒直接存储新生成的伪随机子密码，这无可厚非，只要S盒初始化过后（打乱后）K盒就没什么用了。这一部分对应题目代码如下（题目是用一个新的列表放子密码的，即O）

def OO0o(self, length):
        O = []
        for _ in range(length):
            self.Ooo = (self.Ooo + 1) % 256
            self.oO0 = (self.oO0 + self.O0[self.Ooo]) % 256
            self.O0[self.Ooo], self.O0[self.oO0] = self.O0[self.oO0], self.O0[self.Ooo]
            t = (self.O0[self.Ooo] + self.O0[self.oO0]) % 256
            O.append(self.O0[t])
        print(self.O0)
        return O

之后就是加密过程，就是用我们最后得到的那个子密码来和明文做异或，得到密文。对应下面这段代码

def xor(s1, s2):
    return bytes(map((lambda x: x[0] ^ x[1]), zip(s1, s2)))	# zip会返回一个元组的列表，返回列表长度与最短的对象相同	
xor(msg, O0O)	# O0O就是上面return的O

到此，题目的加密过程完毕，输出了最后的S盒和密文

这道题感觉难就难变量定义的稀奇古怪，让人没有看下去的欲望，如果分析不下去了建议休息会再看，不然真的脑壳痛（恼）

那么我们要怎么求解明文呢？就要用到异或的知识。密文是通过异或得到的，要变回去，我们就得知道子密码盒，然后再异或一次就可以得到flag了，所以现在目的是求子密码盒。

这里我们就得考虑flag的格式，我们可以想到flag肯定是以’}’结尾的，这个已知，我们和密文异或，就可以得到一个子密码，即S[t]，知道S[t]以后，我们通过index函数就可以查列表的下标，于是我们就可以知道t

t知道以后我们关注这个式子t = (self.O0[self.Ooo] + self.O0[self.oO0]) % 256我们换种写法可能好看一点t = (S[i] + S[j]) %256，S[i]是已知的（最后一次i就是明文的长度，S盒又是知道的，所以S[i]已知）我们就可以得出S[j]，这样我们通过index就可以知道j，i和j都知道以后我们就可以逆推回去，把每一次的S[t]都算出来，这样和密文异或就可以把明文求出了，可以在纸上写一下，会很清晰

代码如下

s = [166, 163, 208, 147, 181, 152, 69, 90, 253, 114, 150, 255, 218, 220, 34, 74, 63, 201, 70, 115, 233, 96, 43, 169, 103, 191, 14, 149, 143, 25, 105, 93, 199, 246, 51, 75, 20, 5, 107, 3, 52, 135, 111, 139, 113, 47, 184, 76, 161, 174, 23, 30, 173, 72, 198, 56, 85, 55, 106, 126, 244, 223, 104, 29, 112, 148, 219, 118, 165, 59, 98, 175, 125, 100, 17, 16, 108, 6, 214, 140, 130, 206, 89, 62, 4, 236, 251, 91, 28, 45, 18, 53, 1, 144, 193, 133, 73, 44, 57, 88, 250, 204, 177, 67, 120, 21, 79, 71, 2, 185, 211, 200, 65, 234, 117, 9, 226, 142, 230, 209, 132, 248, 242, 196, 101, 81, 238, 247, 119, 179, 131, 229, 94, 50, 22, 183, 24, 158, 190, 222, 155, 172, 19, 12, 225, 10, 189, 232, 146, 227, 212, 210, 31, 164, 138, 78, 122, 176, 121, 0, 194, 186, 162, 160, 188, 168, 216, 153, 37, 252, 127, 145, 33, 82, 58, 170, 61, 254, 136, 207, 8, 237, 159, 36, 239, 95, 178, 167, 182, 102, 27, 123, 60, 129, 42, 26, 99, 39, 97, 40, 235, 205, 7, 49, 202, 197, 109, 195, 245, 171, 180, 15, 46, 83, 48, 156, 92, 249, 38, 32, 203, 41, 124, 54, 217, 134, 154, 35, 157, 128, 137, 221, 84, 86, 215, 213, 80, 11, 116, 141, 241, 64, 224, 87, 77, 187, 68, 192, 151, 240, 13, 228, 231, 66, 110, 243]
a = b"]7\xab\xc9\xd8\x90\x1f\xd2OP\xad\x87'0\xe1\xff=~"


t=s.index(ord('}')^ord('~'))
i=18
sj=(t-s[i])%256
j=s.index(sj)
s[i],s[j]=s[j],s[i]
j=(j-s[i])%256
i=i-1
t=(s[i]+s[j])%256
flag='}'
while i>0:
    flag+=(chr((a[i-1])^s[t]))
    s[i],s[j]=s[j],s[i]
    j=(j-s[i])%256
    i=i-1
    t=(s[i]+s[j])%256

flag=flag[::-1]
print(flag)

# flag{einfache_rc4}

LCG

https://www.cnblogs.com/vancasola/p/9942583.html

https://en.wikipedia.org/wiki/Linear_congruential_generator

LCG入门-CSDN博客

加密流程

LCG（linear congruential generator）线性同余算法由以下参数组成：

参数	m	a	b	X
性质	模数	乘数	加数	随机数
作用	取模	移位	偏移	作为结果

LCG算法是如下的一个递推公式，每下一个随机数是当前随机数向左移动 $ log_2a
$ 位，加上一个 b，最后对 m 取余，使随机数限制在 0 ~ m-1 内

$ X_{n+1}=(aX_{n}+b)\mod m $

只要我们知道上面的重要参数，要求哪个都很轻松，所以要知道以下公式

公式1：反推$ X_n $

$ X_{n}=(X_{n+1}-b)*a^{-1}\mod m $

公式2：求a

$ a=(X_{i-1}-X_{i-2})^{-1}*(X_{i}-X_{i-1})\mod p $

公式3：求b

$ b=(X_{i+1}-aX_i)\mod m $

公式4：求m

$ t_i=(X_i-X_{i-1})=a(X_{i-1}-X_{i-2})=a*t_{i-1}\mod m $

$ t_{i+1}t_{i-1}-t_it_i=a^2t_{i-1}-at_{i-1}at_{i-1}=0\mod m $

上面这个式子就说明了 $ t_{i+1}*t_{i-1}-t_i*t_i $ 是p的倍数，那么我们只要改变i，得到两个值，求一下公因子，就可以求出来m

例题

babyLCG

题目

from Crypto.Util.number import *
from secret import flag

m = bytes_to_long(flag)
bit_len = m.bit_length()
a = getPrime(bit_len)
b = getPrime(bit_len)
p = getPrime(bit_len+1)

seed = m
result = []
for i in range(10):
    seed = (a*seed+b)%p
    result.append(seed)
print(result)
"""
result = [34162247026397342478798569901414759621400, 48622925600981805953284319521855204943516, 873946493924376814098626588792484831751, 55835889122403142019357216062663278735799, 78197983655527534886328482392841803329879, 7826910556079551454813328357787595898220, 48420932174201345880210110234297855524418, 41702494213414751668850237022097487126943, 53964978232593731384060231097661907644428, 41614447441497057710125709202129649216700]
"""

考点：LCG

只要知道关于LCG的三个基础公式，这道题就很简单，建议自己推导一遍

$ seed_i=（a*seed_{i-1}+b）\mod p $

设$ t_i=(seed_i-seed_{i-1})=a(seed_{i-1}-seed_{i-2})=a*t_{i-1}\mod p $

$ t_{i+1}*t_{i-1}-t_i*t_i=a^2t_{i-1}-a*t_{i-1}*a*t_{i-1}=0\mod p $

上面这个式子就说明了 $ t_{i+1}*t_{i-1}-t_i*t_i $ 是p的倍数，那么我们只要改变i，得到两个值，求一下公因子，就可以求出来p，p有了a也很好求

$ a=(seed_{i-1}-seed_{i-2})^{-1}*t_i\mod p $

a有了随便套一个式子就可以求b了，这样LCG的三个重要参数就都有了，第一个值逆回去就可以求出明文了

代码如下

from Crypto.Util.number import *
from gmpy2 import *

result = [34162247026397342478798569901414759621400, 48622925600981805953284319521855204943516, 873946493924376814098626588792484831751, 55835889122403142019357216062663278735799, 78197983655527534886328482392841803329879, 7826910556079551454813328357787595898220, 48420932174201345880210110234297855524418, 41702494213414751668850237022097487126943, 53964978232593731384060231097661907644428, 41614447441497057710125709202129649216700]
t1=result[1]-result[0]
t2=result[2]-result[1]
t3=result[3]-result[2]
t4=result[4]-result[3]
t5=result[5]-result[4]
t6=result[6]-result[5]

p = gcd((t6*t4-t5*t5),(t5*t3-t4*t4))
print(p)
a=(t3*gmpy2.invert(t2,p))%p
print(a)
b=(result[1]-a*result[0])%p
m = ((result[0]-b)*gmpy2.invert(a,p))%p
print(m)
print(long_to_bytes(m))

# flag{gratulieren}