格入门

这两周就是学习了一些格的基本知识，因为临近期中考，学的有点仓促，但总算是了解了一点，我把学到知识点也写了写，作业的解题思路会放在后面题目运用那里，可以跳转去看

一. 预备知识

要学习格，是得有线性代数的知识才行的。（反正我看到那些矩阵向量什么的就回忆起上学期被线代支配的恐惧）因为我上学期线代学的也不好，忘的也差不多了，加上这里篇幅也有限，我也只能点一下cryptohack上面提到的一些线代知识，目前来看够用，不过强烈建议系统的学习一下线代。

向量和向量空间

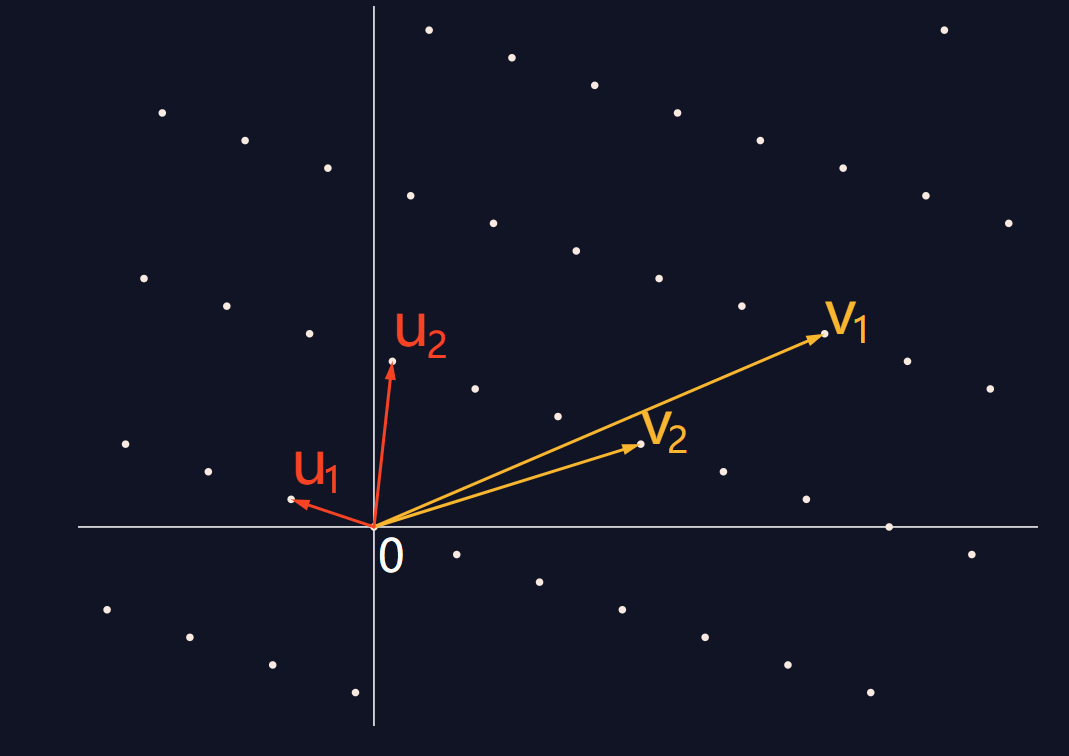
以二维向量空间举例，我们可以任意取一个点A，连接原点O和A点，这就构成成了一个向量。我们也可以用A点的坐标来表示这个向量,就像这样v=(x,y)

向量满足加减、数乘和点积运算，下面举例说明（加粗表示向量）

v=(a , b)，w=(c , d)

v + w = （a + c，b + d） （减法同理）

c * w = （c * a， c * b ） （数乘）

v * w = a * c + b * d （点积）

多维是同理的

然后向量还分行向量和列向量，可以简单理解为行向量就是在纸上横着写的向量（确信），列向量就是在纸上竖着写的向量（确信）

向量大小和基

$ \begin{Vmatrix}v\ \end{Vmatrix} $用来表示向量的长度，其大小是$ \begin{align}
\sqrt{v*v}
\end{align} $(高中应该就有这个知识点的)

这里还有一些关于线性独立的知识点，比如向量空间里有一组向量$ v_i $

满足方程$ \begin{align} a_1⋅v_1+a_2⋅v_2+…+a_k⋅v_k=0 \end{align} $

当$ a_i
$全为零时等式才成立，那么这k个向量就是线性无关的，反之线性相关

而向量空间的基底会要求是一组线性无关的向量，当我们有了这一组向量基，我们就可以用这个基底来表示这个向量空间中的任意向量

拿二维空间举例

$ \begin{align} i=(0,1)\end{align} $ $ \begin{align} j = (1,0)\end{align} $就是一组线性无关的基底，这两个向量就可以表示整个二维平面

其实了解一下矩阵会更有帮助，但是我就不介绍了（有试着想写一下，但是发现讲不清楚，还是留给大家的线代老师吧）

线代课程（放一个宋浩老师线代课的链接吧）

施密特正交化

这个东西感觉只可意会不可言传了，我就放个图，大家自己悟吧（主要我也不知道为什么，只会套公式）

这个正交化就是可以构造一个正交基，正交的概念就是向量相互垂直，上面我举的二维空间的基底就是一组正交基，因为点乘为零（两个向量垂直，点乘为零）

正交化会有挺多好处的（应该，反正没学懂，就会套公式）

这个就是解决一下crypto hack上的一道题，其他地方好像和那个高斯晶格规约有点像，但那里我们会四舍五入，所以还是有点区别的

下面放一个求解代码

1
2
3
4
5
6
7
8
9
10
# sage
from sympy.matrices import Matrix, GramSchmidt
l = [Matrix([4, 1, 3, -1]), Matrix([2, 1, -3, 4]), Matrix([1, 0, -2, 7]), Matrix([6, 2, 9, -5])]
# 注意：将数据转为Matrix格式，否则调用GramSchmidt函数会报错！
# 返回未单位化结果
o1 = GramSchmidt(l) # 注意：orthonormal默认为False，不执行单位化操作
print(o1)
# 返回单位化结果
o2 = GramSchmidt(l,orthonormal=True) # 注意：orthonormal设为True，执行单位化操作
print(o2)

二. 格的初步认识

参考文档

格攻击之小未知数方程求解入门——原理与例子 | Tover’s Blog

这个博客里讲的真的很好！

格定义

这里先放一个课本上的定义

可能看起来比较难懂，但是我们还是从上面那个二维平面出发，我们已经知道了我们可以用一组基底来表示整个二维平面（基底不唯一），我们是通过把这两个向量乘以不同的系数后相加得到的，那么想象一下，我们如果令系数只为整数会怎么样呢？

这个时候，我们通过这个基底，就只能得到空间里的一些点，那么这个就是一个整数格

我们把基底写成一个矩阵，那么就可以得到上面定义里的写法，同时这个矩阵的行列式的值，叫做这个基本域的容积

同时如果我们扩展到n维向量空间，就是定义里的表示

格常见问题

通过上面我们简单了解了一下格是什么，长什么样，那么就要考虑能拿它干什么

这就得提一下格上的两个常见问题，一个是最短向量问题（SVP），另一个是最近向量问题（CVP）

SVP是指我们要在格L上找到一个最短的非零向量$ v $，使得$ \begin{Vmatrix}v\ \end{Vmatrix} $最小

可能在二维空间里你一下就可以看出来哪个是最短的向量，但是一旦扩展到多维时，这就是一个困难的问题了。这里补一个课本上看到的存在性定理，感兴趣可以看一下

那么为了找到这个最短向量，我们有以下规约

高斯格基规约

这个是适用于二维平面，通过算法可以找到二维平面里的最短向量，感觉是LLL的特殊情况（因为好像sage上用LLL的算法也可以解这个），下面放个算法图

如果你仔细看一下的话就会发现这个算法和那个施密特正交化是有一点像的，但是我们知道在施密特正交化里，m不一定是整数，这就会导致得到的向量不在格里，所以我们对m四舍五入取整，这样来得到

LLL格基规约

原理其实感觉差不了太多，就是去找最短向量

这里的运用就是根据关系找到一个基底的矩阵，矩阵中所有数是已知的，然后我们要求解的向量（要求解的未知数构成的向量）是一些数作用在这个矩阵后得到，这个向量就在格上，然后我们期望这个向量是最短向量，以此来求解未知数，下面放一个newstar时候用过的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# sage
from gmpy2 import *
from Crypto.Util.number import *
#from tqdm import *
 
a = 134812492661960841508904741709490501744478747431860442812349873283670029478557996515894514952323891966807395438595833662645026902457124893765483848187664404810892289353889878515048084718565523356944401254704006179297186883488636493997227870769852726117603572452948662628907410024781493099700499334357552050587
b = 1522865915656883867403482317171460381324798227298365523650851184567802496240011768078593938858595296724393891397782658816647243489780661999411811900439319821784266117539188498407648397194849631941074737391852399318951669593881907935220986282638388656503090963153968254244131928887025800088609341714974103921219202972691321661198135553928411002184780139571149772037283749086504201758438589417378336940732926352806256093865255824803202598635567105242590697162972609
 
 
mat = [[b,0],[a,1]]
M = Matrix(ZZ,mat)
qq,pp= M.LLL()[0]   # 最短向量
 
print(pp)
print(qq)

然而要运用LLL算法是有条件的，就是我们要通过这个算法来求最短向量，那么我们要求的向量起码得是最短向量，这就得看一下上面的最短向量存在定理，我们要求解的向量长度满足条件后才是最短向量，才可以用LLL算法，然后格的维数也不能太高，不然准确度不高，耗时也会长。

具体解一下题应该就能理解，可以往后看

三. 题目及运用

我们来具体分析一下下面这一题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from Crypto.Util.number import getPrime, inverse, bytes_to_long, long_to_bytes
import random
import math

from Tools.scripts.var_access_benchmark import make_nonlocal_writer

FLAG = b'crypto{?????????????????????}'


def gen_key():
    q = getPrime(512)
    upper_bound = int(math.sqrt(q // 2))
    lower_bound = int(math.sqrt(q // 4))
    f = random.randint(2, upper_bound)
    while True:
        g = random.randint(lower_bound, upper_bound)
        if math.gcd(f, g) == 1:
            break
    h = (inverse(f, q)*g) % q
    return (q, h), (f, g)


def encrypt(q, h, m):
    assert m < int(math.sqrt(q // 2))
    r = random.randint(2, int(math.sqrt(q // 2)))
    e = (r*h + m) % q
    return e


def decrypt(q, h, f, g, e):
    a = (f*e) % q
    m = (a*inverse(f, g)) % g
    return m


public, private = gen_key()
q, h = public
f, g = private

m = bytes_to_long(FLAG)
e = encrypt(q, h, m)

print(f'Public key: {(q,h)}')
print(f'Encrypted Flag: {e}')

因为我在newstar的时候有简单看看格，那个时候认识不够全面，以为只要构造出一个矩阵就行，所有下面分享一个错误思路

就是我一看到就定睛在e = (r*h + m) % q这个式子上

然后e - m = q*k + r*h

所以$ \begin{align}(k,r)\begin{pmatrix}q&0 \\ h&1 \end{pmatrix} =(e-m,r)\end{align} $

我们写成 v*B = w

想着这个式子构造出格，直接求明文，简单简单

但是这个思路是错误的，因为没有考虑我们通过（k，r）作用到矩阵后得到的这个向量到底是不是最短向量

我们可以算一下$ \begin{Vmatrix}w\ \end{Vmatrix} $和$ \sqrt2{det(B)}^\frac{1}{2} $（根据上面最短向量存在定理比较一下，就可以判断w是不是最短向量），其实这里没有明显的算出值（因为我们不知道m，但大概率这个w的长度是大的）所以大小都不知道，我们根本无法判断w是不是最短向量，所有LLL规约求出来的不是w。这里根本还是因为我违背这种题目的初衷，就是本来是用格攻击求小未知数，但是我求的不是小未知数

上面错误思路告诉我们，不是所有的式子都可以通过构造格来求解，只有当我们要求解的未知数所构成的向量恰好在格上，且这个向量恰好是最短向量时（小未知数），才可以求解

那么下面来看正确做法

既然上面那个式子构造出来的格不对，那么我们转战另一个式子

h = (inverse(f, q)*g) % q

即 h = k * q + f -1 * g mod（q）

这么看有个f关于q的逆元，那么两边乘个f，得到

h * f = k * q * f + g

我们试着移项得到 g = h*f + k1 *q*f （为什么要移项？因为我们要把已知的两个数h和q放在一边，来构造矩阵）

这个时候就很清晰了，加上 kf * 0 + f = f （感觉是一类比较固定的式子，一个恒等式，方便构造矩阵）这个式子就可以得到

$ \begin{align}(k_1f,f) \begin{pmatrix} q&0 \\ h&1 \end{pmatrix} =(g,f)\end{align} $

我们写成 v*B = w

这个时候我们再验证一下$ \left \| w \right \| = \sqrt{f^{2} * g^{2}} ＜\sqrt{(\frac{q}{2})^{2} *(\frac{q}{2})^{2} } ＜\sqrt{2}\sqrt{q}＜\sqrt{2} det(B)^{\frac{1}{2} } $

f和g小于q的一半应该是显然的，因为题目定义的时候就是小于的，不理解可以返回去再看一下题目定义f和g那里

这个时候w大概率就是最小向量，这个时候，我们运用LLL格级规约就可以求出w，即密钥，然后通过解密代码（题目已给）就可以求出明文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# sage
from gmpy2 import *
from Crypto.Util.number import *
#from tqdm import *

a = 2163268902194560093843693572170199707501787797497998463462129592239973581462651622978282637513865274199374452805292639586264791317439029535926401109074800

b = 7638232120454925879231554234011842347641017888219021175304217358715878636183252433454896490677496516149889316745664606749499241420160898019203925115292257


mat = [[b,0],[a,1]]
M = Matrix(ZZ,mat)
g,f= M.LLL()[0] 

print(f)
print(g)

def decrypt(q, h, f, g, e):
    a = (f*e) % q
    m = (a*inverse(f, g)) % g
    return m
    
Publickey=(7638232120454925879231554234011842347641017888219021175304217358715878636183252433454896490677496516149889316745664606749499241420160898019203925115292257, 2163268902194560093843693572170199707501787797497998463462129592239973581462651622978282637513865274199374452805292639586264791317439029535926401109074800)
q = Publickey[0]
h = Publickey[1]
e = 5605696495253720664142881956908624307570671858477482119657436163663663844731169035682344974286379049123733356009125671924280312532755241162267269123486523


g = 43997957885147078115851147456370880089696256470389782348293341937915504254589

f = 47251817614431369468151088301948722761694622606220578981561236563325808178756

m =decrypt(q, h, f, g, e)
print(long_to_bytes(m))

就可以解出明文了

四. 总结

最后简单总结一下用格解小未知数方程的过程

首先找到一个式子，转化成一个向量（感觉可以叫系数向量，因为就是这个向量作用于矩阵，以此来得到一个在格上的向量）乘以一个矩阵（基底），得到另一个向量（我们要求解的小未知数所构成的向量）的形式

然后可以简单判断一下是不是最短向量（根据最短向量存在定理）

之后就可以用LLL规约解出最短向量，这个向量里的就是我们要求的小未知数了。